
평면, 초평면 등 다중 차원을 사용하여 다변량 데이터를 한눈에 살펴볼 수 있다. 함수 f(x, y, z) = x + y + z에서 여러 입력 특성을 조합하는 것처럼 말이다.
이변량 그래프
콘서트를 보러 가는 데에 드는 총 비용이 다음과 같다고 해보자.

위와 같이 콘서트를 보러 가는 데에 고려해야 하는 품목이 두 개가 되면 전체 세 차원 중 입력 특성은 차원 두 개로 표현된다. 만약 티켓 가격과 비어 가격, 주차비가 각각 80, 10, 40으로 정해져 있다면 그래프로 어떻게 표현할 수 있을지 다음과 같이 살펴볼 수 있다.
먼저 데이터를 만든다.
import numpy as np
number_people = np.arange(1,11) # 사람 수 1-10
number_rbs = np.arange(0,20) # 음료 수 0-19
# numpy 도구를 이용해서 두 배열의 외적을 구합니다.
number_people, number_rbs = np.meshgrid(number_people, number_rbs)
total_cost = 80 * number_people + 10 * number_rbs + 40
이제 데이터를 여러 가지 각도에서 살펴본다. 다음은 같은 그래프를 다섯 가지 관점에서 그려보는 코드이다. 이는 평면(plane)의 형태로 그려질 수 있고, 이 평면의 기울기는 각도에 따라 달라 보일 수 있다.
# 'projection':'3d' 를 위해 라이브러리를 임포트해야 합니다.
from mpl_toolkits.mplot3d import Axes3D
fig,axes = plt.subplots(2, 3,
subplot_kw={'projection':'3d'},
figsize=(9,6))
angles = [0,45,90,135,180]
for ax,angle in zip(axes.flat, angles):
ax.plot_surface(number_people, number_rbs, total_cost)
ax.set_xlabel("People")
ax.set_ylabel("Beverages")
ax.set_zlabel("TotalCost")
ax.azim = angle
# 마지막 축은 사용하지 않습니다.
axes.flat[-1].axis('off')
fig.tight_layout()
이처럼 코드와 수식으로는 3차원 표현이 꽤 직관적이지만, 플롯에서는 그렇지 않다. 그 대신 익숙한 몇 가지 도구를 사용해서 출력 테이블을 만들어 볼 수는 있다.
다변량 데이터 테이블
다음과 같이 하나에 $5인 핫도그를 추가해서 콘서트 비용을 계산한다고 해보자.

데이터를 만드는 코드이다.
number_people = np.array([2,3])
number_rbs = np.array([0,1,2])
number_hotdogs = np.array([2,4])
costs = np.array([80, 10, 5])
columns = ["People", "Beverages", "HotDogs", "TotalCost"]
np_cartesian_product라는 함수로 numpy 배열을 이용해서 모든 가능한 조합을 만들어 테이블로 표현한다.
costs = np.array([80, 10, 5])
counts = np_cartesian_product(number_people,
number_rbs,
number_hotdogs)
totals = np.dot(counts, costs) + 40
display(pd.DataFrame(np.column_stack([counts, totals]),
columns=columns).head(8))
위의 np.column_stack함수는 점곱을 하기 위한 코드이다. 점곱을 통해 변수 totals의 계산을 쉽게 할 수 있고, 계산하는 코드를 전혀 수정하지 않고도 비용과 개수를 임의로 확장할 수 있다.
np_cartesian_product함수를 구현하는 코드는 다음과 같다.
# the difference with a "raw" np.meshgrid call is we stack these up in
# two columns of results (i.e., we make a table out of the pair arrays)
def np_cartesian_product(*arrays):
''' some numpy kung-fu to produce all
possible combinations of input arrays '''
ndim = len(arrays)
return np.stack(np.meshgrid(*arrays), axis=-1).reshape(-1, ndim)
+1 트릭

위와 같이 복잡한 수식을 사용할 때에는 보통 상세한 변수 이름을 제거하고 알려진 값을 일반 식별자로 대체하여 추상화한다.

코드에서는 한발 더 나아가 wx합을 점곱으로 대체하여 표현한다.
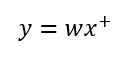
여기서 x+는 1이 곱해진 w0 열이 추가되었다는 의미이다. 이를 +1 트릭이라고 한다.
+1(플러스 원) 트릭을 이용하여 테이블에 담긴 데이터를 다루어보면 다음과 같이 나타낼 수 있다.
다음과 같은 D = (x, y)라는 테이블이 있다고 하자.

여기서 수학적 편의를 위해 +1 트릭을 반영한 D와 x를 쓰곤 한다.

Reference
마크 페너, <머신 러닝을 다루는 기술 with 파이썬, 사이킷런>(길벗, 2020)
'AI' 카테고리의 다른 글
| [Machine Learning] 범주 예측: 분류 모델 생성 과정 (0) | 2020.10.21 |
|---|---|
| [Machine Learning] 선형 결합, 가중 평균, 제곱합, 오차 제곱합 (0) | 2020.10.14 |
| [Machine Learning] 머신 러닝에서 알아야 할 확률 개념 (0) | 2020.10.12 |
| [Machine Learning] 머신러닝이란? (0) | 2020.10.09 |